Background
Project Summary: This project (playfully named “Al-Gore-Rhythm”) is an augmented-reality music theory toolkit designed to make visible some of the more abstract, yet foundational, aspects of music theory. Specifically, I wanted to address the challenging concepts of intervals (the distance between two notes) and triads (the three notes that form certain types of chords).
Context: Harvard Graduate School of Education prototype project (Spring 2019)
Technologies: Unity, Vuforia SDK, C#, iOS, Lasercutter, Inkscape
Duration: 1 week
Inspiration and Influences
For this project, I drew inspiration from three big ideas:
(1) structurations and restructurations,
(2) humane representations of thought, and
(3) the tonnetz diagram.
Structurations and Restructurations
In a 2010 paper titled Restructurations: Reformulating Knowledge through New Representational Forms, Uri Wilensky and Seymour Papert argue that the representational structure and properties of knowledge in a given learning domain (such as math or music) affect its learnability. Furthermore, some learning domains naturally lend themselves to certain types of representations that could be restructured according to both the affordances of a particular medium and the epistemic capabilities of its learners.
Put formally, they define a structuration as “the encoding of the knowledge in a domain as a function of the representational infrastructure used to express the knowledge”, and a restructuration as “a change from one structuration of a domain to another resulting from such a change in representational infrastructure.”
You are now probably thinking: “Umm, okay. Those words sound really cool and expensive, but I have no idea what they mean.”
Fear not, for fear is the mind-killer.
A great example given in the paper is the shift in numeric representations (i.e., a writing system or the symbols used for expressing numbers) from Roman numerals to Hindu-Arabic numerals. In this case, the shift occurred in a learning domain that we can loosely refer to as “mathematics.”
The shift from the Roman numeral “CCCXLVII” to its Hindu-Arabic numeral equivalent “347” can be a considered a shift from a structuration to a restructuration due to a fundamental change in the representational infrastructure of numbers.
In today’s language, we might say that the representational infrastructure of Roman numerals is more “alphabetical” (i.e., it uses alphabetic letters), while the representational infrastructure of Hindu-Arabic numerals is more “numerical” (i.e., it uses what we now very naturally call “numbers”).
Structuration
CCCXLVII
Restructuration
347
To make things a bit more clear, we might even say that the representational infrastructure of tally marks (or hash marks) is composed of the lines that we call “tallys” . The number “347”, then, would be expressed as the following using tallys:

As a restructuration, the Hindu-Arabic numerals provided a new way of structuring, organizing, and expressing a “number”. Furthermore, this new restructuration affected its learnability because of the new types of thinking that it naturally affords. One way of looking at the change in learnability through this shift in numeric representation is by appreciating each in terms of their trade-offs – that is, the advantages and disadvantages that each offer for thinking and doing things with numbers.
For example, using the more “textual-based” numeric representation of Roman numerals, it would be very difficult to handle large, complex arithmetic operations because the Roman numeral system does not have a good way to represent place values (and there is no zero, yet!). In fact, for complicated arithmetic tasks, Romans instead used the “high-tech” abacus.
Under the Hindu-Arabic system, not only was there an increase in the learnability of arithmetic operations such as subtraction, for example, but the new restructuration opened up all sorts of other new ways of thinking about numbers. These new ways of thinking greatly increased and extended the epistemic capabilities (i.e., the range of what we can come to know) of numbers and mathematics itself.

Taking this example further, if we grant some anthropomorphic qualities to our machines, we can consider the use of binary in computers as a sort of restructuration: a new encoding of numeric representations that are good for extending the epistemic capabilities of computers, but not humans. Seen this way, the Roman numeral expression “CCCXLVII” is restructured as “347” for humans and as “000101011011” in binary for computers.
As astutely pointed out in the paper, Hindu-Arabic numerals were not invented with any “educational intent”, but the point here is that they could have been. Successfully restructurating a learning domain such that it increases its learnability will require “deep disciplinary knowledge, creativity in the design of representations, and sensitivity to the epistemological and learning issues” of that learning domain.
Humane Representations of Thought
This idea of a successful restructuration’s sensitivity to the epistemological and learning issues of a particular domain lends itself very naturally to the ideas expressed in Bret Victor’s great 2014 talk titled The Humane Representation of Thought. One of the key benefits of engaging in restructuration-oriented learning design is that it bypasses the problem of pre-requisite skills and knowledge by allowing novices to access and appreciate levels of understanding that would typically be reserved for more intermediate or experienced learners within a given learning domain.
For example, let’s consider the two concepts I tackled in this project, both the interval and the triad. I chose these two concepts because, as a self-directed/self-taught guitarist, I frequently ran into the challenge of trying to understand why music worked the way it did. There seemed to be invisible rules with a system somewhere governing the reason why a key signature is made up of certain chords, why a chord is composed of certain notes, and why certain notes made up a particular scale.
The more I tried to grasp the nature of these rules, the more I hit this invisible wall of arbitrariness. Nothing ever clicked because I was missing some elusive concept — I did not know what I did not know. One day I serendipitously (that is, through YouTube’s autoplay) stumbled across a video on something called “intervals” and I immediately knew that this was not just a missing piece in a puzzle, but rather the keystone piece that would magically make visible a new doorway of understanding.

The problem, however, is that when I tried to dive deeper into the concept of musical intervals, I found that most definitions took the following forms:
“A musical interval is the distance in pitch between any two notes.”
“Intervals are a measurement between two pitches, either vertically or horizontally.”
“An interval is the difference between two pitches measured by half steps.”
Unless you are a bat (see Nagel’s “What’s It Like to be a Bat”) or Geordi La Forge equipped with a VISOR, the idea of a particular sound or tone having a distance is not really intuitive to most humans; that is, humans cannot visually perceive the distance between sound waves. However, if we were designing a music theory lesson for a human-bat-hybrid-chimera-thing (a Bat-Person), then we may very well want to focus on restructurations around such representations of sound waves, as these would be epistemically appropriate for our Bat-Person’s echolocational capabilities.
Alas, unfortunately for us mere humans, the words “distance”, “vertical/horizontal”, and “half-steps” connote the properties of distinct physical objects. We cannot simply pluck immaterial sounds out of the air, alchemically deconstruct them into smaller constituent parts, and then “sound bend” them so that we might explore how they function in various musical contexts (but that would be really neat):

We are faced with similar challenges for the words used in the various definition of triads:
“Triads are made up of 3 notes played on top of each other.”
“A triad is a set of three notes (or “pitch classes”) that can be stacked vertically in thirds.”
Here we again find words that connote more properly the properties of physical objects: “on top of each other”, “stacked vertically”, and “in thirds”. But we also find something slightly contradictory: the word “triad” may itself intuitively connote a “triangle”, instead of just “three of something”. Yet, the descriptions here of notes “stacked on top of each other” or “stacked vertically” is the language of something non-triangular and something more linear.
So there seems to be a misalignment of structurations here: the representational infrastructure of the words used to describe intervals and triads reflect more the physical or tactile world, while the actual representational infrastructure of music is more naturally auditory or aural.
But then from where do these descriptions originate?
A Short History of Standard Notation
The sorts of descriptions of abstract musical concepts described above are so prevalent because intermediate or expert musicians often forget what it’s like to be a novice, so they quite naturally use terminologies that implicitly refer to some intermediary. What’s worse is that they have not only already internalized this intermediary both aurally and visually, but have even mapped this intermediary in practice to their respective instrument(s).
The intermediary from which all these more tactile descriptions of abstract musical concepts emerge is, of course, standard musical notation. For example, diagrams like the one below typically accompany the definition of intervals:

Similarly, when we look at the diagrams that typically accompany definitions of triads, we can immediately understand where the language of “stacked thirds” comes from, as the notes are literally stacked on top of each other when represented in standard music notation:

While references to standard musical notation may seem natural to many, the interesting thing is that standard musical notation is not the natural order of things — it is itself a restructuration!
Much like how Roman numerals and Hindu-Arabic numerals are particular ways of expressing numbers, standard musical notation is just a particular way of representing, notating, and communicating the language of sound that evolved over centuries of innovation and refinement.
Modern standard musical notation started with an initial major breakthrough innovation which was…well, just some lines on paper.
Wait, really? Just some lines on paper? Yes, really.
The staff lines we are so accustomed to seeing today were a major innovation that developed in response to solve problems related to the disadvantages of something we might call Neumatic notation.
For centuries, chants and other monastic tunes (monky tunes?) were transmitted orally since there was no good way to record music. If you wanted to learn a new song, you typically had to learn it in person from someone who already committed the song to memory and then rely on your own memory to practice. (While you might think that doesn’t sound too bad, not all music during this period were modern pop laboratory-made earworms with catchy melodies).
As the number of songs/chants that one had to commit to memory increased, various forms of music notation eventually developed as attempts at standardization. These early attempts were some of the first ways of recording music.
In the Western context, European monasteries developed a way of notating chants using nuemes, which first began as symbols (squiggly-looking marks) that were placed above text to signify the melodic inflections of the syllables in chants/songs. Interestingly, they bear a striking resemblance to Arabic diacritics.

In terms of its learnability, Neumatic notation functioned mainly as a mnemonic – that is, neumes served as a memory aid used to jog the memory of a learner who already knew the song. The teaching of songs was typically done by rote: a monk’s training involved memorizing many of these monky tunes by heart. Those who were experienced and familiar with songs reinforced them through many, many repetitions, which involved years of study (this incredible time commitment was probably seen as an act of devotion).
Yet still, for beginners it would be notoriously difficult to learn a new piece. The neumes were too ambiguous when trying to learn and practice on your own, as they did not contain enough information for someone who was not already familiar with it.
Imagine practicing a piece all night trying to decipher squiggly neumes that merely approximated how the melody would move over a word, only to show up at music practice in the morning and have a domineering monk painstakingly correct every incorrect inflection in your voice:

Fortunately for many young monks in training, a Benedictine monk named Guido of Arezzo would transform the ways in which singing was learned and taught. Guido, (most likely) the innovator of staff notation, had the bright idea of adding these neumes to (colored) lines in order to clarify the exact pitches for a piece of music.
Notes could now be visually encoded by their position in relation to the fixed lines. Although this new staff notation would undergo many more changes, we can consider the shift from Neumatic notation to Staff notation as a major restructuration that not only revolutionized the teaching of singing, but also its learnability.

When Guido began to use his staff lines, he remarked that:
“a piece written in neumes without lines is like a well that lacks a rope to reach the water.”
People could now sing a tune that had never been heard before just by looking at paper! The new representational infrastructure of simple staff lines that Guido implemented afforded the ability to encode and store musical information on something external to the mind and body.
Furthermore, this innovation extended the epistemic capabilities of novices. Instead of an oral tradition with direct imitation of the teacher and treacherous consultation of squiggly neumes to (re)jog their memory, students could now practice effectively and precisely on their own.
Just as Hindu-Arabic numerals led to the handling of complex arithmetic operations, Staff notation similarly led to the composition of more sophisticated music, since it was now possible to offload and store musical information/memory to paper.
The most complex of these compositions would be created by a new sort of specialist, “the composer”, whose predetermined and meticulous creations would gradually eclipse the more improvisational style of skilled musicians.

absolutely real colorized image of Guido de Arezzo after inventing staff notation, ca. 10th Century (just kidding)
We could even say that this particular restructuration helped Guido conceive another of his major innovations: the solfege (what we now consider the “do-re-mi”), which he developed by using the well-known hymn Ut Queant Laxis. He took the first syllable in each line of this hymn to create the hexachord, or six note scale (ut, re, mi, fa, sol, la).
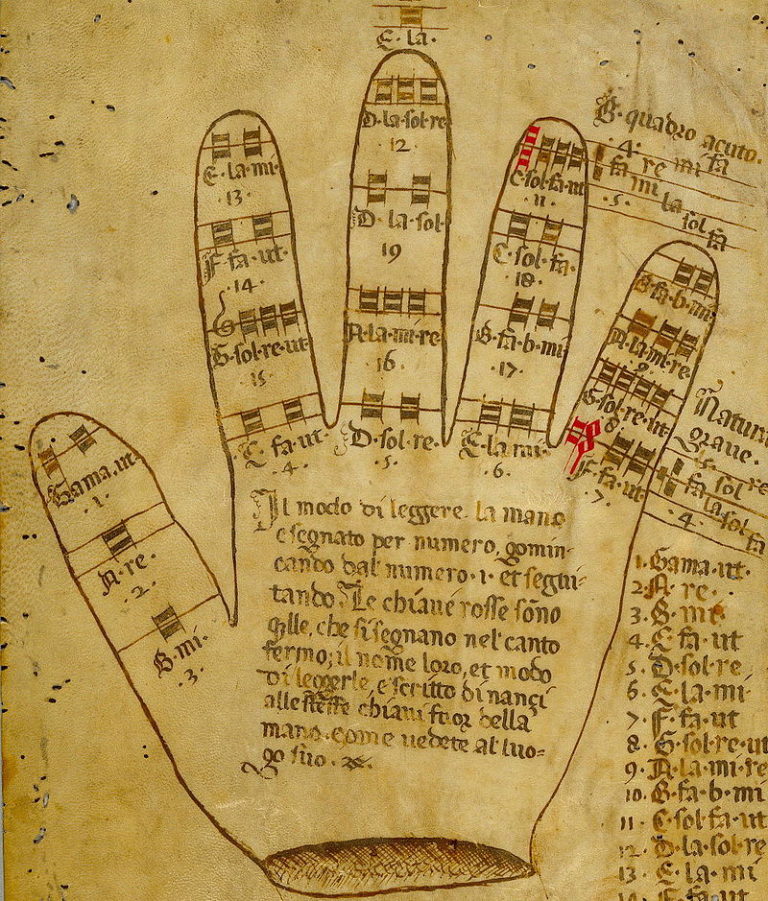
In addition, although historians now believe he did not develop it himself, another innovation called the Guidonian hand was widely used during the time. It was yet another mnemonic used to assist in the teaching and learning of singing. The lines on the finger joints were used to represent specific notes so that one could practice three octaves of the hexachord scales that ran the gamut (this is actually where the word “gamut” originates) from the lowest note in the scale (i.e., gamma ut) to the highest — again, without any paper!
I really wonder how this caught on. Did they run out of paper (i.e., vellum) because it was too expensive and so had to improvise (pun intended) a means of teaching? Did someone notice that Guido’s major innovation, a series of lines, were also present on every human hand and therefore was a natural form of standardization? Or maybe someone tried to cheat on a singing test and wrote down the answers on their hand!
Regardless, it was, and still is, a very intuitive way to apply Guido’s other pedagogical innovations and assist singers in sight-singing:
Although Guido’s innovative staff lines would undergo many changes over time, in the Western context it has remained the standard, especially as it developed alongside the dominating medium of print. But standard musical notation also had its criticisms over the years. For example, the Italian composer Ferrucio Busoni lamented the rigidity of notation in his 1907 Sketch of a New Esthetic of Music:
“Notation, the writing out of compositions, is primarily an ingenious expedient for catching an inspiration, with the purpose of exploiting it later. But notation is to improvisation as the portrait to the living model. It is for the interpreter to resolve the rigidity of the signs into the primitive emotion […] But the lawgivers require the interpreter to reproduce the rigidity of the signs; they consider his reproduction the nearer to perfection, the more closely it clings to the signs.“
As described above, while Hindu-Arabic numerals were not invented with any educational intent, Guido’s innovations were, in fact, invented with educational intent. Guido was motivated by the learnability and teaching of music, not the overly prescriptive notating and recording of it. He would probably turn in his grave if he could read Busoni’s comments on how his his pedagogical innovations, initially conceived and designed to help students learn and love music, had ultimately led to the over-reliance and bureaucratization of it, at least from Busoni’s point of view:
“To the lawgivers, the signs themselves are the most important matter, and are continually growing in their estimation; the new art of music is derived from the old signs—and these now stand for musical art itself.”
Busoni’s frustrations with “the lawgivers” reflect the sentiments of many who wished to break out and away from the rigidity of standard notation. If alive today, he might be surprised to find that there are several software solutions that can creatively capture compositions through digital representations of instruments and then seamlessly translate them directly to standard notation.
Is Standard Notation a Humane Representation of Thought?
Now that we know a bit more about the history and development of Standard notation as a restructuration of Neumatic notation, we can now assess in what ways it may or may not be a humane representation of thought.
I think that Standard notation’s triumph historically reflects the concerns of the print medium, as its utility in encoding, storing, and communicating the language of sound was indispensable while print dominated the world. It not only allowed for the offloading of one’s memory to an external thing (i.e., paper), but allowed musicians of different instruments to communicate through a common and standardized language.
For this reason, standard notation will probably continue to go unchallenged. Even in a brave new digital world, Standard notation continues to be consistently incarnated in a wide variety of digital media. In a sense, it has too many “users” globally and therefore functions as a sort of legacy technology that would be too costly to replace. In fact, the restructuration I designed was not intended to replace Standard notation, but rather to serve as a supplement – an addition to an ecosystem of structurations.

However, what I am arguing here is that Standard notation’s learnability when it comes to the teaching and learning of foundational concepts in music theory is extremely prohibitive, inaccessible to novices, and is therefore not a humane representation of thought. Trying to teach a novice about intervals or triads using Standard notation is like trying to teach an abstract concept in particle physics using a foreign language that they do not understand.
As mentioned above, phrases like “stacked thirds” and intervallic “distances” all implicitly refer to the Standard notation (re)structuration. You first need to be able to decipher this structuration of music in order to understand the various descriptions of music theory concepts on which it is based.
While some (mostly intermediate or experts) can “hear” the notes just by looking at sheet music – novices cannot. In fact, novices need to first map the structuration of Standard notation to an instrument (including the voice, if singing) before reducing their cognitive load enough to readily grasp concepts like “stacked thirds” and “distances between notes”.

what experts see and hear
The saddest part is that the interval and the triad are extremely powerful ideas in music theory. Learning and mastering them as soon as possible is incredibly useful as they are the fundamental building blocks upon which other concepts are built. Unfortunately, the prohibitive nature of Standard music notation, far from intuitively capturing the representational infrastructure of music, usually turns most novice learners away.
Tonnetz
While I do not think Standard notation is going anywhere, there continue to be many attempts to represent and visualize the language of music. Due to music’s universal and subjective nature, it is unsurprising to find so many different attempts at visually capturing it. In fact, many of these music visualizations take on the form of extremely abstract experimental art, which are all neat and very cool…but typically they only make some sort of sense to intermediate or experts within the learning domain of music.
Put in the language of restructurations, the representational infrastructure of abstract music visualizations reflect more the subjective experiential nature of music, having little, if anything, to do with increasing its learnability.
On the other hand, the tonnetz, (German for “tone network), is a restructuration that does increase the learnability of some music theory concepts and was thus incredibly influential in my design. First conceptualized by the mathematician Leonhard Euler, the tonnetz has its own long history of development (e.g., there is even a Vogel’s Tonnetz that extends Euler’s original formulation).
However, the essential features of the tonnetz have stayed the same. It is typically described as “a conceptual lattice diagram for representing tonal space”. Translated for non-musicians, it is a sometimes color-coded diagram that spatially represents pattern-like relationships among musical notes. The tonnetz is commonly used as tool for thinking about and visualizing chord relationships in classical Western music.
Even upon first glance at a tonnetz digram, we find its representational infrastructure to be more inviting than Staff notation. Although very plain-looking by our standards, Guido’s innovative staff lines were the key design feature in its representational infrastructure. Put another way, the laws or rules governing how Standard notation works are embedded in the lines themselves, including the interstitial spaces they create. Without the arrangement of these lines and spaces, Standard notation loses its power as a restructuration that increases learnability.
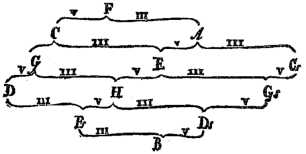
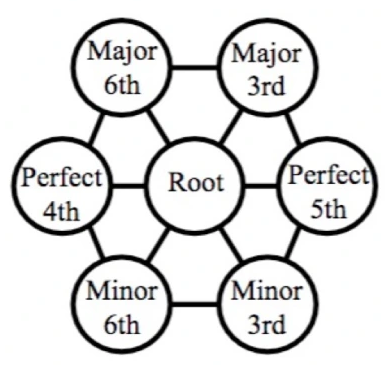
The tonnetz, on the other hand, is arranged into a matrix-like diagram, or lattice, instead of a linear series of lines. Beyond the shapes and colors, the representational infrastructure of the tonnetz is actually governed by a series of intervallic relationships:
Wait, wait…what is this “circle of fifths” of which you speaketh? (Great point! This is the limitation I will describe later).
For now, imagine we took the game Chinese Checkers (or Sternhalma) and modified the rules such that a piece can only move in a certain direction if it satisfies some condition. Much like how pieces in Chess are prescribed to only make certain movements (e.g., the bishop can move any amount of spaces diagonally), we can prescribe some “intervallic rules” on how a piece can move to adjacent spaces on this Sternhalma-looking tonnetz board.
For example, from a particular starting point, which we can call “the root” starting position, moving to the right is always “a fifth” and moving down and to the right is always a “minor 3rd”.
the “rules” of the Tonnetz
chinese-checkers/sternhalma

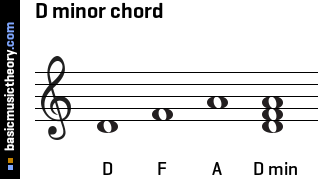
The laws or rules governing the Tonnetz are these intervallic relationships described by the moving of one of these “pieces”. In this way, by moving one “space” to the right (i.e., a fifth) and another down and to the right (i.e., a minor 3rd) we can construct what is called “a minor triad”. In fact, in a Tonnetz diagram, a minor triad is always represented as an upwards-pointing triangle.
This is essentially how the Tonnetz notation restructures Standard notation with a new representational infrastructure:
D minor in Tonnetz Notation
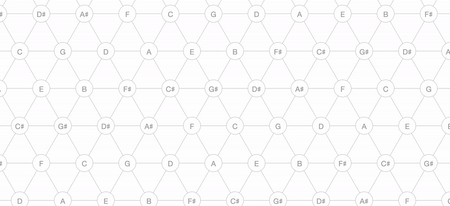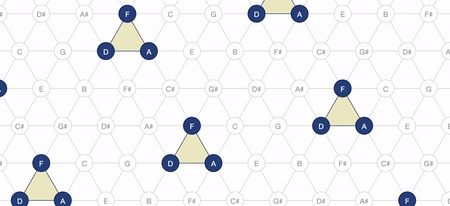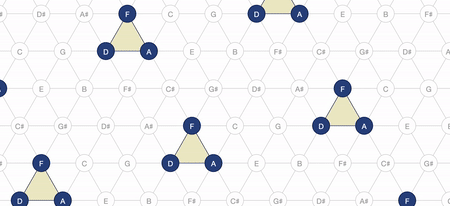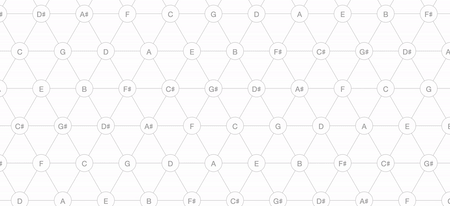
The appeal of the Tonnetz to a variety of music theorists over the years was this way of representing tonal distance and tonal relationships governed by the “intervallic rules” described above. For this reason, I consider the tonnetz to be a powerful restructuration, as it intuitively expresses foundational concepts of musical harmony in a way that is more accessible to novices than is Standard notation, and thus increases its learnability.
Limitations of the Tonnetz
While I find the tonnetz to be an incredibly intuitive restructuration that affords great gains in learnability, it is not very learnable in the sense of deeply exploring the specific music theory concepts I have identified above: intervals and triads. If you were lost during my description of intervals above, it’s because the tonnetz is itself structured upon another music theory concept called the circle of fifths (briefly described above), that presumes you already understand or know about intervals:

And so, to truly appreciate the beauty and design of the tonnetz, you need to already know about the intricacies of the circle of fifths, since the tonnetz actually creatively restructures the circle of fifths. It is this limitation which makes the tonnetz inaccessible to complete novices.
My learning design choices, described below, does not presume one knows anything about the circle of fifths – in fact, I wanted to design something to help a learner discover the circle of fifths for themselves.
The circle of fifths limitation aside, Ondřej Cífka created an amazing interactive tonnetz that you can physically interact with and even “play”. Instead of just a representation of a static diagram, you can also explore the tonnetz as an instrument with real-time feedback and even visualize the harmonic movement of an entire piece of music, moving far beyond depictions of triads:
Erik Satie’s Gymnopédie No. 1 expressed in Standard Notation and as a Tonnetz:
Structuration
Restructuration
Yet, one problem with this interactive tonnetz is that its inputs are all mixed up.
Interacting with this tonnetz on a computer requires the use of a QWERTY-designed keyboard, which itself is in dire need of restructuration. Much like standard notation, QWERTY is a legacy technology that is unlikely to change. (What’s worse is the fact that most of us type using our 2 thumbs on a mobile-based version of a QWERTY-keyboard and it could be argued that the QWERTY-keyboard was “optimized” for 2 hands and 10 fingers – but that’s another story).
Even in futuristic sci-fi worlds, we cannot escape QWERTY-based keyboards:

“futuristic” keyboard in Blade Runner 2049
A concern with the interactive tonnetz is that one might develop misconceptions about the musical alphabet (e.g., C, D, E, F, G, A, B, C, etc.) and its relationship to the alphabetic letters on the QWERTY-keyboard (e.g., A, S, D, F, G, etc.). For example, you would have to press the “A” key on the QWERTY-keyboard to produce a “C” note on the tonnetz, but press the “H” key to produce an “A” note. (An added difficulty here is that if you are a non-native English speaker, your keyboard may be laid out differently or you may use an “H” note for what is typically the “B” note.)
One way to overcome this limitation was the attempt to map the notes to a digital representation of a piano-keyboard; but again, you would already need to know how notes are represented on a piano to gain any understanding from the mapping. In fact, in the piano digram from the interactive tonnetz below, the letter “A” denotes the “C” note on a piano, but a complete novice would not know this:

One last limitation of the tonnetz, even the interactive version, is that complex theoretical aspects of music (such as the circle of fifths) are already baked into its design, and are therefore hidden from the learner. The tonnetz does not really let you experiment with intervallic structures that go beyond the “intervallic rules” outlined above.
In the same way that we cannot pluck immaterial sounds from the air and “sound bend” them, a learner cannot take apart the tonnetz to explore relationships outside of how it is prescribed.
Learning Design
Learning Goals Summary
As I mentioned above, one of the key benefits of engaging in restructuration-oriented learning design is that it attempts to bypass the problem of pre-requisite skills and knowledge by allowing novices to access and appreciate levels of understanding that would typically be reserved for more intermediate or experienced learners within a given learning domain.
With the limited time and resources allotted to me, my learning design goals were thus mainly concerned with creating something that could expose a complete novice to some of the most fundamental properties of music theory, while also allowing them to probe, ask questions, and even discover for themselves some of the tonal representations contained in the tonnetz.
Instead of abstract descriptions using loaded terminology that implicitly referred to Standard notation, I wanted to turn musical notes/tones into actual distinct physical objects that one could move like puzzle pieces and use as interchangeable parts. In a sense, I set out to “de-structurate” the tonnetz diagram and re-organize it based on more fundamental principles that did not assume much knowledge of music theory. Furthermore, to solve the mixed inputs issue of the interactive tonnetz, I wanted to create something that leveraged the most natural of inputs: human hands.
Successful restructurations also involve an awareness and sensitivity to the epistemic learning issues of a particular learning domain. The epistemic sensitivities of sound and music were explored at length through the historical analysis of several musical structurations in the sections above. My learning design tried to address these sensitivities in two main ways:
First, my design does not presume knowledge of any musical instrument; that is, the representations of concepts would be instrument agnostic. I did not want any particular instrument (which are designed things in themselves with their own representational infrastructure) to dictate how these music theory concepts were first encountered and subsequently digested by the learner.
Put another way, I was trying to design something that would serve as a Platonic Form of music theory concepts, their instantiations ultimately taking on different forms depending on the musical instrument. My hope was that a learner would form mental models that would be much more readily mappable to either other forms of musical notation, or even directly to their own instrument.
The second sensitivity I wanted to address was the ability to explore, make mistakes, and sound bad. So much of learning anything musical involves not only making frequent mistakes, but immediately hearing those mistakes in the form of real-time aural feedback. Correcting these mistakes (intended or unintended) while learning or playing an instrument is a key part of the learning process.
One of the capabilities afforded by using augmented reality in this project is the ability to see and hear tones in a variety of novel (and mistake-ridden) circumstances. While the tonnetz is an amazing restructuration, it is restrictive in the sense of only allowing mistakes to occur within its own design architecture. In what I have designed, a learner is not restricted to the lattice layout of the tonnetz, nor the “intervallic rules” which govern it.
Structuration(s)



Proposed Restructuration

Tactile Notes
One of the challenges highlighted throughout the history of music’s structurations was the attempt to “hold” the sound of a tone or musical note in some sort of intermediary. Whether it was on paper/vellum, in one’s voice/body, or how one interacted with notes through an instrument, this recurring problem restricted the learnability of certain musical concepts. Many of the attempts to store musical information in various ways were actually attempts to lighten a learner’s cognitive load enough such that a learner might be able to recruit higher-order cognitive functions when engaging with complex and often abstract musical ideas. Put more simply, externalizing musical information to objects outside of the mind freed up one’s “mental bandwidth” to explore more complex ideas.
During the design phase, I kept wondering what it might look like to not only represent a note/tone without resorting to an intermediary, but how I could create the conditions such that a learner could directly “touch” a sound and manipulate it in the service of learning powerful musical ideas. I initially wanted to use representations of frequency waves, but I abandoned this idea due to time and material constraints.
Although I made clear several times that I was not creating a new type of instrument for making music, many of my classmates viewed it as such. I consistently maintained that I was making a supplementary cognitive tool — an interactive addition to a series of already existing musical representations. Interestingly, I received so many questions about this that it led to a strange realization: musicians produce tones from playing their instrument, they do not directly “touch” them.
This connected quite well to one of the sensitivities I was addressing; namely, that this was an instrument agnostic approach. I started to take the comments that people thought it was an instrument as a good sign. It seemed to suggest approachability and positive sentiments towards music theory, instead of the dread that usually accompanies it.
Phrases like the “distance between two notes” could now be readily seen, heard, and felt. A learner could now physically “pick up” notes and literally construct a triad. If a learner wanted to “pick up” a note and walk or hop it across a scale to count the “half-steps”, they could now do so.
Perhaps such an activity would lead to using their full bodies to internalize intervallic distances, as beautifully demonstrated here:
demonstrating intervallic distances by hopping with the whole body
One other advantage of using tangible physical pieces that are instrument agnostic is that the learner becomes an explorer and theorizer of music.
Like the tonnetz, a learner will still have the ability to hear the tones aurally when interacting with the notes via augmented reality. Unlike the tonnetz, however, the learner here becomes a co-designer in the sense that they are not restricted to the “intevallic ruleset” (i.e., the circle of fifths) of the tonnetz. In fact, if cleverly and appropriately scaffolded, the learner, like Euler, can discover some of the same principles of the tonnetz for themselves.
Furthermore, because what I have designed is less restrictive than the tonnetz, a learner can also discover and form all sorts of theories about music that may be meaningful to them at a particular time and within their current skill level. For example, if someone is currently learning about extended jazz chords on the guitar, they can simply use this tool to form theories and literally (de)construct these chords to see how they work.
In this sense, I hoped my design would have a low floor (easy to get started), wide walls (multiple pathways), and a high ceiling (affording progressively complex interactions over time).

that feeling when you finally touch a musical note
Well-Ordered Problem Solving and Contrasting Cases
Two of my favorite learning design principles that fit well with restructurations and humane representations of thought are well-ordered problem solving and contrasting cases.
Well-ordered problem solving can be described as a problem-solving first approach that sequences problems such that they lead to generative learning outcomes. Doing this well, as explained above, requires a sensitivity to the epistemic issues of a learning domain. Generative learning helps learners “actively make sense of the material so they can build meaningful learning outcomes that allow them to transfer what they have learned to solving new problems.”
I have explained above why intervals and triads are the fundamental building blocks of music theory (at least in the Western context), which is precisely why I chose them as the subjects of my restructuration. They are not only generative principles in themselves, but mastering them can lead to even greater understanding in handling more complex music theory topics.
Similarly, within a given learning domain, contrasting cases can foster an appreciation and help develop a sensitivity for the types of problem solving one is likely to encounter in that learning domain. They help expose a learner to the deep structural issues of a learning domain (sort of like developing a spidey-sense or intuition) so that they can “tune” into these ideas when solving problems. Much like generativity, contrasting cases help lead to transfer and preparation for future learning in a variety of novel problem-solving contexts.
I combined these two ideas by creating the conditions through which a learner could solve well-ordered problems using contrasting cases. By examining side-by-side presentations of two different problem solving contexts, a learner could compare and contrast each and highlight the differences. Instead of making these apparent by presenting facts about them (such as how they are expressed in standard notation), I tried to turn them into visible things. Without contrasts, it’s often difficult to see which parts of an example are important for problem-solving.
For example, each musical scale can be seen as a problem-solving context, since the point of knowing about a musical scale is to employ them meaningfully and artfully in various musical contexts.
Due to the limitations of the wooden sheet I was using, I focused on the most basic and foundational ideas: intervals and how different intervallic values are used to construct different scales.
In terms of deep structures, I wanted to expose the learner to the sensitivity of the third interval — that is, how a tiny change in just the third could transform the entire character of a triad/chord. My hope was that the learner would come to see third interval as the nucleus of a triad/chord and be able to exploit that sensitivity in various musical contexts.



In one example scenario, a learner might go through the following steps:
- Notice the infinitely repeating nature of the musical alphabet.
- Place all 12 notes/tones chromatically in place at the very top and experiment with hearing different intervallic distances.
- Construct the major scale by physically moving pieces down and matching their intervallic values into a pre-defined formula (while noticing which pieces do not move, or which intervals are not included in the construction of that scale).
- Construct a major triad by then removing only the intervals from the major scale that make up a major triad.
- Notice which intervals are “still left on the board.”

After a similar exploration with the contrasting case of the minor scale, the learner may notice that only one note changes when going from a major to minor triad/chord. Well now the learner could ask, “by how much does it change?” or “what intervallic distance is traversed?”
By referring to the formula on the board, the learner can literally see the change in intervallic distance and form a mental model of this change before internalizing it aurally.


Challenges
Technical Challenges
Board Design
I created this prototype as a final project for a course called Digital Fabrication and Making in Education, which took place in the EIS makerspace studio. What I actually had in mind was something much more ambitious, but since I only had about a week and limited access to materials, I decided to commit to this wooden sheet type material. Though limiting, it actually forced me to get creative in fleshing out some of the most important and foundational learning design goals.
Although I first thought of creating a fire-breathing dragon with “scales” and having the chromatic intervals aligned across its back and its tail so that it could breathe musical fire…
…I instead thought I’d just play on the words “steps” (e.g., one typically says “a B note is a half-step away from a C”) by representing the intervals on a chromatic “staircase”.
However, given the dimensions of the material I was working with, I was unable to find room for the well-ordered problem solving and contrasting cases goal described above. I eventually settled on the design seen in the images above.


first board design iteration
Tracking
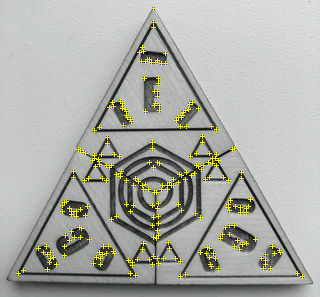
The most time-consuming challenge was related to tracking the pieces that I designed and lasercut. I used Vuforia’s augmented reality SDK so that a learner could use a smartphone to interact with some of the notes and gain access to additional information.
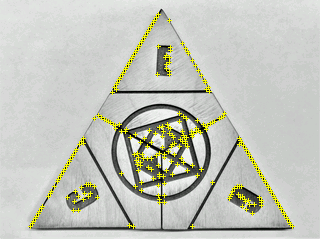
In a nutshell, Vuforia’s SDK takes any image and translates it into a “QR-code” so that 3D digital content can be overlaid on top of it. Vuforia first detects what they call “feature points” in an uploaded target image and then assigns it a rating based on its “trackability”. Vuforia outlines the best practices for an exemplary image target below:

At first, my image ratings were very low, as they did not have enough unique feature points. Eventually I settled on a design that seemed to work just fine:

However, the problem was that I wanted to afford the learner the ability to not only interact with each distinct note, but also the ability to take those three distinct pieces and form different triad-chords by swapping them interchangeably. The newly formulated triad-chord would thus constitute a new fourth image that needed to be uploaded as an image target.
The issue with the bullseye-type design above is that any combination of notes would always create the same bullseye at the center — it was a repetitive pattern.
I needed each unique piece to not only be distinct, but also to form something entirely new when combined. I played around with several designs and finally settled on something that worked:
During this iterative process, I discovered that Vuforia was picking up burned blemishes from the laser cutter and even the imperfections from the wooden pieces themselves. I spent hours sanding these tiny things like a madman to make them as smooth as possible before uploading them to Vuforia’s engine as a target image. You can see more precise and uniformly distributed feature points on the final iteration:
Reflection
Personal Reflection
During the public fair where I presented my design along with classmates, I received a lot of good feedback. Many wondered why I chose the design I did; I simply replied that I had predefined learning goals and these were the material constraints I was presented with. (I also explained what I actually wanted to make if I had a lot of money and time).
However, I noticed that I received the most scathing feedback from classically-trained musicians who were already well-versed in standard notation. It was really quite interesting because when I replied that standard notation was also just a human creation, most defended it as if it was holy writ — as if standard notation came first and music theory emerged from notation, not the other way around.
Anyways, I also always consistently maintained that this could/should be used as a scaffolding tool should anyone want to read standard notation. It could act as a bridge or interpreter of two complex languages. I also suggested that it was just a tool in a suite of already existing tools — a way to develop simple yet powerful mental models of triads and how they are constructed from intervals.
Technical Reflection
While augmented reality is certainly very cool, so many “educational uses” focus way too much on the technology side of things. Whenever technology is introduced into a learning context, it is really hard to define and measure where the learning happens during any sort of interactive activity because learning is something that emerges over and above its constituent parts.
I typically think of learning design goals as having a center of gravity — what is doing the pulling and and why?
The center of gravity of what I designed here is the physical board and the movement of pieces, not the augmented reality. Not only is the form factor of a smartphone awkward with AR experiences, I designed it so that an expert can use this as a teaching tool without augmented reality.
In fact, once a beginner learned how to construct a triad, I did not presume they would even need to use augmented reality anymore (unless they wanted to hear the tones). My hope was that a learner would consult it every now and then when their instrument (or notation) was getting in the way of developing a robust mental model of what is going on theoretically.
Future Work
I may revisit another AR iteration as the technology gets better and the form factor improves. I will surely be including an engaging storyline and to make the restructuration more meaningful in a narrative-based context (dragons!?) — but that’s top secret, sorry.